Understanding Logic Gates - The brains behind Digital Electronics
In the world of digital electronics, everything runs on 0s and 1s. And the magic behind processing these binary values? Logic Gates. From microprocessors to memory chips, every digital device you use is built using these basic building blocks.
Primary Logic Gates:
- They are called "primary" because they are the basic building blocks of digital electronics.
- These gates perform the most fundamental logical operations
⮞ AND Gate:(Multiplication-like)
- The output is 1 only if both inputs are 1.
- Boolean Expression: Y = A·B
- The output is 1 if any one or both inputs are 1.
- Boolean Expression: Y = A + B
⮞ NOT Gate:(inversion)
- It inverts the input.
- Boolean Expression: Y = A̅
Why Primary?
Because all other complex circuits and logic functions are ultimately built from combinations of these three basic gates. They are the "first" layer of logic.
Universal Logic Gates:
- They are called "universal" because you can use only one type of them to build any logic circuit.
- NAND and NOR gates are universal.
Using only NANDs or only NORs, you can make AND, OR, NOT, and any other logic circuit.
⮞ NAND Gate (NOT + AND):
- It is the complement of the AND gate.
Boolean Expression: Y =
⮞ NOR Gate (NOT + OR)
- It is the complement of the OR gate.
- Boolean Expression: Y =
Why Universal?
Because they are powerful enough to "universally" implement any logic function without needing other gates.
Derived(Secondary) Logic Gates:
- They are called "derived" because they are created by combining primary gates.
- These are secondary gates formed from the basic ones
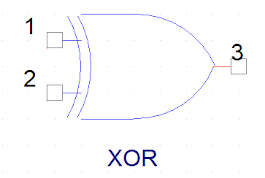
⮞ XOR Gate (Exclusive OR):
- Output is 1 if only one input is 1.
- Boolean Expression: Y = A̅B + AB̅
⮞ XNOR Gate (Exclusive NOR):
- Output is 1 if both inputs are the same (either both 0 or both 1).
- Boolean Expression: Y = AB + A̅B̅
⮞ NAND gate (NOT + AND)
⮞ NOR gate (NOT + OR)
Why Derived?
Because you derive them (create them) using primary gates.
- Primary = Basic ingredients (like flour, sugar, salt)
- Derived = Recipes made using the ingredients (like cake, cookies)
- Universal = A super ingredient (like magic powder!) from which you can make any recipe alone!
Boolean Algebra and Expression Simplification:
Boolean Algebra is used to simplify complex expressions and reduce the number of gates in a circuit.
Some important laws:
A + AB = A (Absorption Law)
A(A + B) = A (Absorption Law)
A + A = A
A · A = A
Tip:
For more than three variables, you can use K-Maps (Karnaugh Maps) to make minimization faster and easier — a vital skill for logic designers!
In Short:
- AND, OR, NOT are the primary gates.
- NAND and NOR are the universal gates.
- XOR and XNOR are derived gates.
- Boolean algebra helps simplify and optimize designs.
- Truth tables define how a gate behaves for each input combination.
Coming up next in the Digital Series: Number Systems Conversion - stay tuned to hobitronics.blog














As NAND as well as NOR gates are both universal and derived as we get it from NOT + AND , NOT+OR , but leaving gates (eg) in CMOS technology , we can implement NAND , NOR logic using pull up and pull down network .... then can it still be a derived gate or will that behave as a basic gate?
ReplyDeleteIn CMOS technology, NAND and NOR behave as basic gates because they are directly implemented using pull-up and pull-down networks, even though functionally they are derived (NOT + AND/OR) in Boolean logic.
Delete